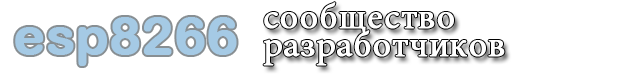Прикидычно функция на пару страниц asm для типового DSP. На Cortex ещё как-то перенесется, но возможно будет тормозить если нужна особая точность (старт показаний после 3-х секунд замера и удержание фазы с вычислением частоты на каждый smps). На ESP лучше и не думать реализовывать...
Все это знаю не только по книжкам, и не только преподавал это, но и делал реальные системы обработки испытаний того что летает.
А то что период первой гармоники будет совпадать с периодом пульсовой волны - это вообще-то азы спектрального анализа.
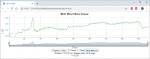
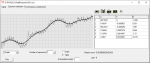
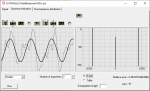
Но в целом, красивые у вас картинки.
-----------------------------
Относительно применения вейвлет, тут я с вами не соглашусь.
Вообще-то для таких задач используют
метод Карунена-Лоэва, который нашел применение в диагностике заболеваний и прогнозирования послеоперационных осложнений еще в прошлом веке.
--------------------------
Потом его стали использовать в социал. исследованиях поведения и классификации толпы ну и т д
А указанный вами метод можно рассматривать как его упрощение, но с таким же успехом упрощением является и ДПФ.
---------------
Но вопрос в том, что Вы дальше будете делать с полученными коэффициентами.
-----------------------------
Любой математический метод - подобен мясорубки
на входе мясо - на выходе фарш
на входе г-но - на выходе оно же.